内啡肽:冷静作用
促进内啡肽分泌的方式:运动,冥想,深呼吸,笑
多巴胺:预期奖励
短期大量释放多巴胺,让我们更追求短期快感,更没耐心。
更多的多巴胺或提高阈值,导致更难获得快乐。
保持平常心,减少情绪波动,降低多巴胺分泌。
差不多退役了
算法竞赛教会我什么呢
多年之后还能影响到我的估计只有思维上多出的一丝敏捷(这都没有就啥都没有了
吉老师线段树什么的怎么可能记得呢(亏我熬夜到一点去调代码,结果是思维方式有问题
(把tag放在一起考虑,
要是有机会去wc的话,接下来一段时间的目标是数学和dp
有机会了(这是你颓废那么多天的结果吗。。
1.$n$维曼哈顿距离可以变成$2^{n-1}$维契比雪夫距离。(相当于枚举$n-1$个的符号)
2.三分:(2l+r)/3,(l+2r+2)/3
3.对时间建线段树可以代替cdq分治
4.二进制分组
5.离散化:sort+unique+lower_bound
sort(a+1,a+n+1);
n=unique(a+1,a+n+1)-a-1;
查值x:
return lower_bound(a+1,a+n+1,x)-a;
或者
6.hash:模$2^{31}+1$,设后31位为a,前面为b,原数为$a+b*2^{31}$,模完为$a-b$
7.压位
8.区间众数
离线:莫队 $O(n\sqrt{n})$ 右端点递增;左端点固定,每次向左移到询问的位置,结束再撤回(回滚莫队)
在线:(1) 分块+vector二分 $O(n\sqrt{nlogn})$
(2) 分块,对每种值在每个块末尾记录出现次数,$O(n\sqrt{n})$
9.dtx: 倍增替代二分
10.二分图中:最小点覆盖等于最大匹配(最小点覆盖$\geq$最大匹配,且每个匹配中取一个点可以成为点覆盖)
最大独立集+最小点覆盖=点数(独立集是点覆盖的补集)
11.符号:%的值同被除数,/的值根据被除数和除数的符号,相同为正,不相同为负
12.[k/i]一共根号个值,下一个i=k/(k/i)+1
可以用到整除分块的形式,大致是这样的:
$$ \sum_{i=1}^{n}[\frac{n}{i}] $$
from peng-ym
这个式子,O(n)计算是非常显然的。但,有的时候因为多组数据的要求,可能O(n)并不是正确的时间复杂度。那么这个时候,我们就有一种O($\sqrt{n}$)的做法。这就是:整除分块!
对于每一个⌊n/i⌋我们可以通过打表(或理性的证明)可以发现:有许多⌊n/i⌋的值是一样的,而且它们呈一个块状分布;再通过打表之类的各种方法,我们惊喜的发现对于每一个值相同的块,它的最后一个数就是n/(n/i)。得出这个结论后,我们就可以做的O($\sqrt{n}$)处理了。
附一个整除分块的代码吧:
13.printf输出double是四舍五入的,保留两位向下取整就-0.005+eps再输出,向上取整就+0.005-eps再输出
double有15位有效数字
eps应该是小于你能算出来所有数两两之差(xy)
精度误差可以认为在[-1e-13,1e-13]之间
何时+/-eps凭感觉(xy)
只能详细记录各种情况了:
(负数的四舍五入要看题目定义,故只讨论正数)
拿边界往里带
正数的四舍五入要+eps,(负数可能要-eps)
14.尺规作图只能做加减乘除开方五种运算
15.隔板法要么是隔数字要么是隔位置
16.线性求逆元:inv[i]=(p-p/i)inv[p%i]%p或者inv[i]=p-p/iinv[p%i]%p;
inv[1]=1是一定要写的!
17.最大团和最大独立集是等价的,都是npc
一个图的最大团和取反的图的最大独立集等价
18.高维前缀和要一位一位做
集合的子集和和高维前缀和一样
要一位一位做
否则会重复
001<-000
010<-000
011<-001
<-010
然后发现000在011中出现两次、
应该是
001<-000
011<-010
010<-000
011<-001
19.坐标范围1到n的下凸壳上有sqrt(n)个点
20.A坐标系中的切比雪夫距离=B坐标系中的曼哈顿距离
A坐标系中的曼哈顿距离=B坐标系中的切比雪夫距离(B为A旋转45°,顺时针和逆时针是一样的,因为在互相垂直的坐标系中切比雪夫距离和曼哈顿距离是等价的)
旋转45°,(x,y)->((x+y)/2,(x-y)/2)
曼哈顿距离:dis=|x1−x2|+|y1−y2|
切比雪夫距离:dis=max(|x1−x2|,|y1−y2|)
将一个点(x,y)(x,y)的坐标变为(x+y,x−y)(x+y,x−y)后,原坐标系中的曼哈顿距离 == 新坐标系中的切比雪夫距离
将一个点(x,y)(x,y)的坐标变为((x+y)/2,(x−y)/2)((x+y)/2,(x−y)/2) 后,原坐标系中的切比雪夫距离 == 新坐标系中的曼哈顿距离
21.无向仙人掌图判定:dfs+差分,返祖边的下端点+1,上端点-1,一条边属于>2个环就不是仙人掌,否则是。
有向仙人掌图判定:dfs,找到一个环就暴力的把环上每条边+1
22.$T(n)=2T(n/2)+O(n) => O(nlogn)$
$T(n)=T(n/2)+O(n) => O(n)$
$T(n)=4T(n/2)+O(n) => O(n^2)$
23.处理与询问无关可以用分治
24.打决策点看决策单调性
25.一定要造极限数据!!把int全换成ll再跑一遍看结果之类的。
26.两遍dfs找树的直径不适用于负权(证明需要每条边大于等于0,还是dp管用)
例子:(1) -> 1 -> (2) -> -2 -> (3) -> 2 -> (4),从2开始就爆炸了
27.$\sum_{i|n}n/i=O(n)*质因数个数(n)$
28.开根复杂度:O(loglogn)牛顿迭代复杂度
29.p1+p2=1则模意义下p1+p2=1(mod p)(要求:设p1=a/b(没有约分时),(a,p)=1,(b,p)=1)
30.在剩下的数中等概率选,可以等价为:不减少数,在所有数中等概率选,选中不合法的无收益,重来
证明:
$F=\frac{1}{n-1}(f(1)+…+f(n-1))$
$F=\frac{1}{n}(f(1)+…+f(n-1))+\frac{1}{n}F$
显然两式等价
31.treap的删除要注意,删到不存在的节点要停住,不然tle(cjq)
32.rand用48271ll*seed%INT_MAX可以生产1到INT_MAX-1的所有数
33.结构体中的函数可以调用该结构体后面的函数,结构体中不能声明函数。
正常的函数如果出现循环调用要先声明。
34.集合s
遍历s的子集 for(int i=s;i>0;i=(i-1)&s)(没有枚举空集
int x=s;
while(1){
solve();
if(x==0) break;
x=(x-1)&s;//只有x是s的子集的时候是有效的
}
遍历s的超集 for(int i=s;i<Max;i=(i+1)|s)
35.最短路计数(先判掉0环)
spfa:每次更新后要清0
dijk:不能处理0边?(无0环)
36.dag上dp:拓扑出来或者记忆化搜索,spfa会t啊。
37.可并堆的3种写法:
1.左偏(dist_left>=dist_right)
2.无脑换
3.随机换
38.单调上升转成单调不降通过ai -> ai-i
单调不降转成单调上升通过ai -> ai+i
39.最短路:边多:不加优化的dijk
边少:加堆优化的dijk
40.树上背包有时可以转化成dfs序做(比如必须要是连通的,对于某个点,选就继续,不选就跳过整个子树)
41.有时边存不下仍然是可能可以跑出来的(存边需要乘上一个常数,心中有边即可。。)
42.数组直接做参数会隐式转换为指针,传参的时候a[]和*a是等价的,甚至方括号里写一个长度都是等价的,不过二维或更高维数组只有第一维变成指针
43.手动开栈:-Wl,–stack=/字节数/
-Wl,–stack=1000000000 //开1GB的栈
44.区间加等差数列:维护每个区间加的a+bi(i是第几项)
线段树要求记录的值和tag可以合并
45.bit上的二分:
46.(二维数点)求矩形内点的个数(离线):
按x排序,在y轴上建树桩,遇到矩形的左边界作减法,遇到矩形的右边界作加法
(在线或带修改): bit套权值线段树 //233
47.线段树维护区间gcd:是nlog(做一次辗转相除,gcd减小一倍)
48.noi2016区间,按区间长度排序,左右指针,线段树维护被覆盖的最大值
49.BZOJ 4552 线段树合并?
50.组合数
$(x+1)^n=\sum{i=0}^n({i}^{n})*x^i$
两边求导后令x=1,可以求得一阶和式
再求导可得二阶和式..
卢卡斯定理(p为质数)
当p=2时,$({k}^{n})=0$只有n=0,k=1,$({k}^{n})=1(mod 2)<=>(n and k)==k$
小根堆,确定树的结构,求不同树的个数:$\frac{n!}{\prod_{x=1}^n sz[x]}$
51.区间可减(求和)比区间合并/区间可加性(min/max)条件更强
猫树只需要满足区间合并,不修改
- $$f\big|\bigcup_{i=1}^nAi \big|=\sum{i=1}^nf\big|Ai\big|-\sum{1<=i<j<=n}f\big|A_i\bigcap A_j\big|+…+(-1)^{n-1}f\big|A_1\bigcap…\bigcap A_n\big|$$
53.随机1到i-1作为父亲的树:平均深度O(logn),期望最大深度logn
prufer编码生成树:期望最大深度O(sqrt(n)),期望平均深度O(logn)
54.斯特林数/卡特兰数/划分数怎么用:
卡特兰数:(以下都是等价的)
通项公式1:$Cn=\dfrac{1}{n+1}{C}{2n}^n={C}{2n}^n-{C}{2n}^{n-1}$
通项公式2:$Cn=\dfrac{1}{n+1}\sum\limits{i=0}^n\left({C}n^i\right)^2$
递推公式1:$C{n+1}=\dfrac{2(2n+1)}{n+2}C_n,C0=1$
递推公式2:$C{n+1}=\sum\limits_{i=0}^nCiC{n-i},C0=1$
第二类斯特林数:
通项公式:$S(n,k)=\frac{1}{k!}\sum{j=0}^{k}(-1)^{k-j}(^k_j)j^n$
递推公式:$S(n+1,k)=k*S(n,k)+S(n,k-1)$
划分数:
递推公式:$p(n,k)=p(n-k,k)+p(n-1,k-1)$
55.对一堆询问len[l,r]=k,区间只满足可加性,O(n)做法(在线):在k的倍数的位置划分,向前向后维护一段,每个询问必定过一个划分位置
56.对一堆询问,不存在区间包含,即l1<=l2<=l3<=l4…,r1<=r2<=r3<=r4…,区间只满足可加性,O(n)做法(离线):以r1为划分向前向后做,这样可以处理所有过r1的询问,当li>r1的时候,每次向左扫只需要扫到上次的r,这样每个点只会从左边和右边各扫一遍
57.可持久化线段树的区间修改:要开2log的空间(因为每层访问最外边的两个节点),标记永久化,每次经过都加上标记即可
58.启发式合并复杂度O(nlognlogn)每个数只会被插入logn次
splay/treap/fhq treap合并是nlogn
启发式合并的空间怎么释放?没有浪费空间,只是更新指针所指的位置
59.线段树合并:一开始n个位置,nlogn个节点,时间复杂度nlogn(每dfs一次就减少一个点,一共就一开始的nlogn个点,合并过程中不开新点了),空间复杂度nlogn
60.区间加等差数列,区间求max:分块(线段树不可做)
区间加等差数列,区间求:线段树
61.
怎么ntt?每个链用组合数算,ntt合并
62.S可简单图化:Havel–Hakimi algorithm/Erdős–Gallai theorem
HH是贪心,复杂度O(n^2logn)
EG是结论(?),复杂度O(n),?
63.找一个图的所有环?tan90
64.点上打标记:(1)子树和 (2)到根的和
65.n^3/64找最短路(边权为1..)
bitset lowbit?
66.取模,除0:记录有多少个0,每次减
67.答案比状态小可以用答案作为状态
68.决策单调性:
1)dp值已知??分段,先求前面再求后面
2)从1到n依次刷表
栈维护每个决策点和左右端点
69.区间平方和满足四边形不等式(能转化成区间平方之类的大概有可能满足吧)
70.include
71.子集和问题(一些数的和能否为x)
sum(a)<=n,共O(sqrt(n))个不同的数,O(nsqrtn)的多重背包(多重背包不能压位)
或者把sqrtn个东西二进制拆分,变成01背包,变成O(sqrtnlogn),然后bitset优化,O(nsqrtnlogn/w)
对一开始的物品:
2x+1个a => a,x个2a
2x+2个a => a,a,x个2a
这样每个物品不超过2个,变成sqrtn个不同数的01背包
复杂度O(nsqrtn/w)
72.V 1e9 n 100
体积 ai2^bi (a<=10,b<=30)
价值 ci (<=1e9)
bi从大到小排序
dp(i,j)表示到第i个物品,实际容量还有j2^bi+V%2^bi
j最大到sum(ai) (记到1000)
改一下dp
dp(w,j)表示到第w个物品,实际容量还有j*2^w+V%2^w
例题:
1(梦幻岛宝珠)
2体积小的,物品少,V 1e18,完全背包。完全背包的物品可以变成ai2^0,ai2^1…
73.石子合并:有决策单调性,O(n^2) 先按长度dp,每层转移是O(n)
74.合并同余方程:
互质:中国剩余定理
不互质:两两合并(就是解二元一次方程。)推导
75.二次剩余不要搞错:
$x^2=n(mod p)$对每个确定的n在[0,p)上只有一个解
对(p-1)/2+1个n有解
76.((~0)>>1)=-1
((~0u)>>1)=INT_MAX
-x=2^32-x
a^b<=a+b
a^b+2(a&b)=a+b
a^b=a+b <=> a&b=0
或的单调性
(x|y)>=x
77.bitset解决5维偏序(可以解决k维偏序,复杂度:预处理O(kn),每次询问O(ksqrtn))
78.动态加边,求两点路径和?nlogn,启发式合并
79.给定 n 个数 a[1..n],求有几个子集满足:子集的异或和等于这个子集的AND
80.double的二分姿势:不能卡精度,只能卡次数
while(r-l>eps)是错的。。
for(次数)(推荐写法)
while会停不下来(因为mid=(l+r)/2==l)
[-A,A]的外接圆的半径是A^2级别的
二分用sqrt(l*r)可以次数更少。(l,r>0)
函数对long doulbe有单独的版本
89.$[\frac {[\frac{a}{b}]}{c}]=[\frac{a}{bc}]$ 画画线段就能证明
90.knight’s tour:
nn中,n>=5存在哈密尔顿路径,n>=6且n为偶数存在哈密尔顿回路(证明见wiki)
nm中,只要min(n,m)>=5则存在哈密尔顿路径,无证明(搜索证明。。
91.double的三分姿势
int的三分姿势
92.常见npc:
- 哈密尔顿回路(哈密尔顿路径不是,但是依旧没有多项式算法)
- tsp
- 图同构:图G1是否与图G2同构?
子图同构:图G1是否与图G2的任一子图同构?
子图同构问题是NPC,而图同构问题一般认为不是P也不是NPC问题,虽然它明显是一个NP问题。这是一个典型被认为很难却还不是NPC问题的例子。 - 3sat及以上
- 背包
- 一般图染色
- 子集和问题
- 全排列问题
- n皇后问题
常见np-hard: - 求图的最长路
- 一般图最大团
- 一般图最大独立集
常见np: - 拓扑图计数
93.(a|b)+(a&b)=a+b
94.c++03的东西:
95.set
重载方式:
1.直接重载pair的比较方式
在全局写bool operator < (const pii &a,const pii &b)
2.在这个set里面重载
struct cmp{
bool operator () (const pii &a,const pii &b){
}
}
96.a<b,b<c,如果能推出a<c
97.()后的const表示当前结构体,什么时候要用?库函数(不修改this)
friend什么时候要用?有private,和写外面一样
98.模拟退火
爬山(凸函数,也就是只有一座山峰)
99.要对10以内的c敏感 from dtx
100.局部到整体
101.全序关系才能排序,偏序关系只能拓扑排序
102.dijk用堆优化mlogn
用桶优化O(n+m+最大权值),用指针维护(权值递增)
- /:根目录
/home/noilinux/或~/:当前用户的目录
ls:显示当前列表
ls + 路径:显示路径下的列表
cd + 路径:/home(绝对路径) 或 Desktop(相对路径)或 cd ..(返回上一层)
/./:当前路径
/../:上层路径
mkdir:创建文件夹
rm -r + 目录:删除当前目录及里面所有的东西(-r 递归地删)
sf_sharefold和/不是同级的:在/下的某个文件夹内
touch + 文件名:(创建文件)修改文件的修改日期(没有就创建)
cat + 文件 + 文件:(显示文件内容)将几个文件的内容显示出来
mv + 文件 + 路径:将文件移动到路径下
cp + 文件 + 路径:将文件复制到路径下
将文件复制到文件:
1.cp + 文件 + 文件
2.cat + 文件 + >文件
mv和cp 都要加-r才能对文件夹操作
;可以隔开两个命令
echo或printf:输出
\;可以输出;
“”可以把东西搞成字符串
echo + 信息 + >文件:将信息覆盖到文件
echo + 信息 + >>文件:将信息追加到文件后
0:stdin
1:stdout
2:stderr
ctrl+c:退出当前命令
ctrl+z:将当前命令压到栈中
fg:将命令从栈中弹出
ctrl+d:EOF
diff + 文件 + 文件:相同为0,不同不为0
g++
-Wall:显示所有warning
-O0 -O1 -O2 -O3 -Ofast:加速
-g:生成给调试器用的信息
-lm:链接数学库(不加也行)
-o + 文件:输出到指定文件
-std=c++11
-Wl,–stack=/栈的大小,单位字节/
bash + a.sh:用bash运行文件
104.+-1rmq:按len=logn/2分块,对整块作st表,复杂度O(n)
对块内进行预处理,本质不同的块一共O(2^len)=O(sqrt(n))个,对这些块的每个[l,r]都暴力预处理,复杂度O(sqrtloglog)
查询O(1)
105.dag中求:
1)一个点能到的点数:O(nn/32),bitset优化暴力
2)拓扑序的个数:状压,O(2^nn)
106.
%d–> for int
%u–> for unsigned int
%ld–> for long int
%lu–> for unsigned long int
%lld–> for long long int
%llu–> for unsigned long long int
107.char[][](一堆字符串)进行排序:新开一个位置数组,对这个数组排序
108.namespace是个好东西,在namespace里面、函数外面定义的变量还是全局的,除了可以重变量名没啥特别。
109.字符串hash冲突的概率:使用次数^2/模数大小(和生日悖论差不多?),要双hash
110.#define rep(形参,形参,…) 替换列表
例如:
#define rep(i,x,y) for(int i=(x);i<=(y);++i)//记得打括号,不然传1<<n就挂了
111.二维数组传参(int a[x][y])或者(int a[][y]),只有第一维可以不写!
112.rand()是通过线性递推
windows下模32768
rand()%(2^x)有周期,大概1e5
更好的随机数是
mt19937 mt(/随机数种子/);
设置种子的第二种方法:
mt.seed(/随机数种子/);
在
mt19937 mt(time(0));
mt();//返回一个随机数
mt.min();//mt的最小值0
mt.max();//mt的最大值2^32-1
mt19937_64 mt(time(0));
mt();
mt.max();//最大值为2^64-1
注意u和llu输出
113.dijk不用vis每次判断和最小值是否相同即可,pq写大根堆也会得到正确的结果(但是会t)
114.高斯消元复杂度:nmmin(n,m)
115.邻接表判重边:
116.k叉哈夫曼树可以O(n)构造:
桶排,然后用两个队列
k叉哈夫曼树的dp
f[i][j]表示已经做完了前i个元素,还空出j个叶子节点的最小代价
f[0][1]=0,其他为inf
第二维最大为大于n的2的幂
$f[i+1][j-1]=min(f[i][j]),f[i][j*k]=min(f[i][j]+\sum_{p=i+1}^{n}a[p])$
$ans=min(f[n][p])(0<=p<n)$
#458. 我才不是萝莉控呢
这题和哈夫曼树的dp有类似
但是有些不同
将dp的含义改成f[i][j]表示做完前i-1个元素即可
要求的答案也是f[n][1],因为最后放完一定没有空节点
117.tr1是c++03的using namespace tr1;(在using std之后加)
头文件如#include
118.保序回归:
将数列a调整成单调不降的最小代价,a调整为b的代价为|a-b|
调整为单调上升则对ai-=i
原因:
维护的每个点可以到达的最低距离
只有当再次小于最低距离后才要继续更新答案
做法出处:http://codeforces.com/blog/entry/47094?#comment-315161
写的好看的dp:https://blog.csdn.net/Vectorxj/article/details/78793739
仔细思考发现,考虑函数图像并不能很好的解释(或者我太弱了
本质还是维护到达的最低距离
但是原来的理解有些偏差
记f[i]表示考虑[1,i]的答案
那么f[i]是单调不降的
(注意题解中的fi[x]是下凸的,没有斜率为非负的线段)
pq中存的是不改变当前答案的情况下,能变成的最低的情况
因为fi[opt[i]]=fi-1[opt[i-1]]+opt[i-1]-a[i]
所以尽量把opt[i]变小,就是把大的往下拉(注意拉完之后并不是合法的序列,只是保证有1.满足答案2.最大值是opt[i] 的序列)
当所有opt[i]都变小以后,最大值就变小了
反正就是不太容易理解
cjq太强了
cf的做法是维护折线
维护折线一般要维护横纵坐标或者斜率什么的
这题只需要维护横坐标和斜率
一个点和下一个点的斜率为严格比这个点大的点的个数
因为斜率的变化只有+-1
可以通过加点和删点来维护
听完sr的讲解整个人神清气爽,他的题目是树上的,更复杂。
链的做法的解释:
f[i][j]表示前i个数变成单调不降,第i个数为j的最小代价
g[i][j]表示前i个数变成单调不降,第i个数小于等于j的最小代价
f[i][j]=g[i-1][j]+abs(a[i]-j)
g[i][j]=min(g[i][j-1],f[i][j])(g是f的前缀最小值)
sr称这是用函数去表示状态
对每个特定的i,都能画出j-f[i][j]和j-g[i][j]的函数图像
这类函数有两个特点:
1.函数均是下凸壳
2.函数每一段的斜率都是整数(横坐标的差是1)
f函数最后一段的斜率是1,g函数最后一段的斜率是0
通过维护每个横坐标上的数量来维护斜率
比如f函数的点数是1,2,则斜率是-2,-1,1
下面的代码维护了g函数(维护f也行,但是这题维护g比较方便)
新加入的点如果小于最大,则斜率一段-1一段+1
那么最大的数量-1,新加入的点+2
因为f[i][j]最小(也就是f函数中斜率为0)的就是答案,比最大的值小的点加入要把它改成最大,这个差贡献到答案
新加入的点如果大于最大,则最大点之前斜率-1
链的代码:
树上的做法:
f[i][j]表示以i为根的子树中,i向fa[i]连j的边的最小代价
g[i][j]表示以i为根的子树中,i向fa[i]连大于等于j的边的最小代价
f[i][j]=sum(g[son[i]][j])+abs(a[i]-j)
g[i][j]=min(g[i][j+1],f[i][j])(g是f的后缀最小值)
也满足链中的性质:
1.函数均是下凸壳
2.函数每一段的斜率都是整数(横坐标的差是1)
还是维护堆(这次是小根堆)
但是多了sum操作,所以使用可并堆维护g(合并的话就是把堆合并,因为斜率对应的点数也是可加的)
还要维护g在最左边的纵坐标(这是答案,合并的时候直接加)
119.vector
120.一般图四元环:n^3/32
二分图四元环:msqrt(m),分大小点
- 12345678for (int i = 1; i <= n; i++) {f[i] = a[i];}for (int i = 1; i <= n; i++) {for (int j = 2 * i; j <= n; j += i) {f[j] -= f[i];}}
当a[i]=i时,f[i]=\phi(i)
猜一波结论:
$$when\ \varphi(i)\neq
0,f[i]=(\sum{j|i}\mu(j)\cdot a[j])\cdot\mu(i)$$
$$when\ \varphi(i)=0,t=\text{product of every prime factor of i},f[i]=(\sum{j|t}\mu(j)\cdot a[j\cdot\frac{i}{t}])\cdot \mu(t)$$
122.ctrl+m:把dev分成左右两个窗口
123.f[i]表示二进制下是i的超集的数的个数
先枚举某一位j,再枚举i(从小到大和从大到小都可以,因为每一位只有0/1)
f[i^(1<
相当于高维前缀和,每一维只有2
好博客~!
124.对vector
sort(a.begin(),a.end());
a.resize(unique(a.begin(),a.end())-a.begin());
125.a+b=1在模意义下为a+b=1(mod p)
126.求本质不同的子序列个数:
dp[i]表示 1-i 的方案数 , dp[i] = 2*dp[i-1] - dp[pre[i]-1] (pre[i]是之前一个和i颜色一样的位置) from fsr
dp[0]=1;
空子序列也算在里面了,O(n)
127.求区间mex:
1)离线:
有两种:
一、按l从小到大排序,[l,r]->[l+1,r]就是把a[l]删掉,会对r<nxt[a[l]]的询问产生影响,update(l,nxt[a[l]-1,a[l]),即用a[l]去更新最小值
二、按r从小到大排序,last[x]表示x这个值最后出现的位置(到r为止),要找最小的x,使得last[x]<l,线段树上二分
2)在线:主席树
3)带修改:树套树?
128.linux下scanf比较快,跟fread差不多,不需要手写快读(数值大的时候还是要手写快读。)
一定要用getchar快读!!
scanf:
int -> %d
long long -> %lld
unsigned int -> %u
unsigned long long -> %llu
float -> %f
double -> %lf
long double -> %Lf
char -> %c
char a[] -> %s
printf:
int -> %d
long long -> %lld
unsigned int -> %u
unsigned long long -> %llu
float -> %f
double -> %f (和scanf不一样!)
long double -> %Lf
char -> %c
char a[] -> %s
129.小凯的疑惑:
设答案为x
显然存在n,使得x=na(mod b)(0<=n
所以x的最大值在n=b-1,m=-1时取到
130.涉及换根的时候,考虑一开始先把树建出来,将fa[i]等需要的信息预处理出来
131.前缀和的迭代:
f[0]:a1,a2,a3,…
f[1]:a1,a1+a2,a1+a2+a3,…
f[2]:a1,2a1+a2,3a1+2a2+a3,…
对于f[x][y],a[j]对其的贡献系数是从(1,j)走到(x,y)的方案数,为C(x+y-1-j,x-1)
132.分治时对于询问[l,r]所属的mid可以通过将区间变成(0,2^x)这样O(n)-O(1)(预处理-单词询问)
也可以对mid所属的层用st表,这样是O(nlogn)-O(1)
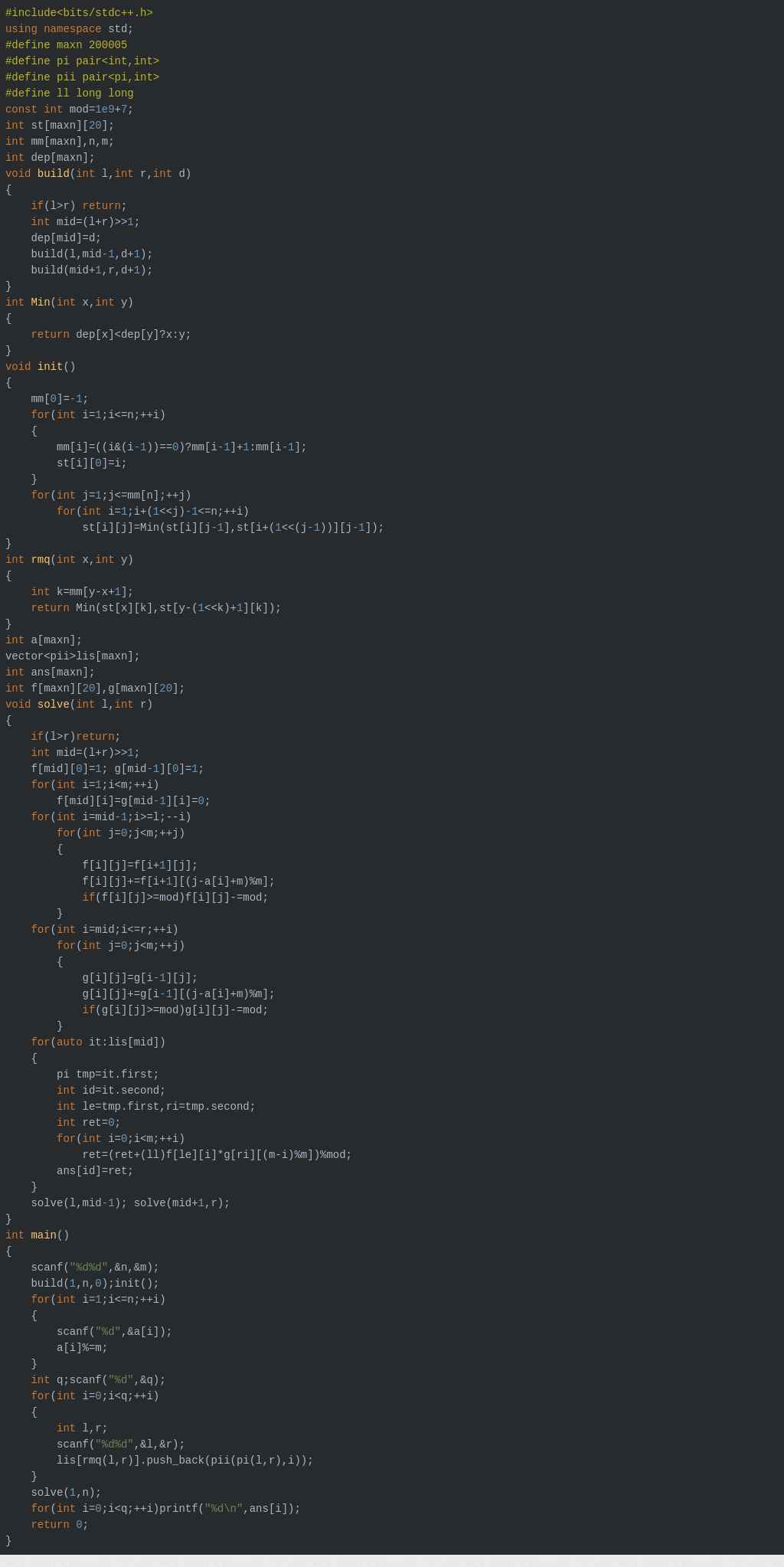
133.fc一样的文件文件大小也可能(一般)不一样!!(linux和windows的回车问题)
134.写启发式合并应该写不写启发式,保证程序正确后,另开副本加入启发式
135.
//映射越少越好,多了容易错
//a[]->b[]和b[]->a[]在写法上还是有一定区别的,要对题目具体分析
//一般是根据跟a[]有关和跟b[]有关的量的特点来处理(比如每次要处理多少个)
//修改的值一般是映射左边的量,不改的(或者修改不方便的)是映射右边的量
//
//bzoj1483 存在原值a[]和真值b[]的映射
//若vector[]以a[]作为下标,则建立b[]->a[]的映射
//若vector[]以b[]作为下标,则建立a[]->b[]的映射
//但是,本题要启发式合并,vector的下标和b[]之间会产生映射关系
//用a[]作为下标,这样相当于b[]->vector[]的映射
136.double一直乘很小的数和一直除很大的数会小于误差范围然后直接输出0
不要除很小的数或者乘很大的数,这样精度丢失严重
- $$\sum{a=0}^{m}(^{m-a}{n})a=(^{m+1}{n+2})$$
考虑组合意义,从m+1里面选n+2个,先钦定第二个选a+1,第一个有a种,后面有C(m-a,n)
$$\sum{k=0}^{m}(^{m-k}_{n-h})(^{k}{h})=(^{m+1}{n+1})~(m,n,h~is~const)$$
138.k叉树i的孩子j(0<=j<k)为i*k-k+2+j
i的fa为(i+k-2)/k
139.atan2(y,x)表示点(x,y)的角度,值域是$(-\pi,\pi]$,(x,0)(x>=0)为0,(x<0)为pi
140.常用的memset
int/LL:
memset(a,0x3f,sizeof(a));//INF
memset(a,0xcf,sizeof(a));//-INF
141.卡常技巧:
1.循环展开对%没什么用,只对+-max等比较快的有用
让%的次数尽量少的出现,不要放在循环的最里面
__int128很慢
2.llu比ll快
142.dinic的复杂度:
- 在存在一层容量都是1的分层图上:$O(E^{1/2}E)$
- 在所有边的容量都是1的图:$O(min(V^{2/3},E^{1/2})E)$
- 在单位网络(除了源汇以外,每个的的入流和或出流和为1)上:$O(V^{1/2}E)$
143.scanf/printf相关:
- scanf的返回值:成功赋值的参数数(在首个参数赋值前发生匹配失败的情况下可为零),或若在赋值首个接收的参数前输入失败则为EOF。(EOF=-1)
while(scanf()==个数)//!=EOF在存在垃圾输入的时候可能会出错 - scanf(“ %c”,&c);可以过滤下一个字符之前的所有空格回车tab
144.priority_queue按照重载的<进行从小到大排序(没重载就按默认的大小关系)
std::less
std::greater